환급미션 50일째
소프트웨어 베이직 - 자료구조와 알고리즘 - 17. 그래프 - 너비 우선 탐색
소프트웨어 베이직 - 자료구조와 알고리즘 - 18. 탐색 - 이진 탐색 트리
운영체제 - 가상 메모리의 이해 - 페이징 시스템
운영체제 - 가상 메모리의 이해 - 다중 단계 페이징 시스템과 페이징 시스템 장점
운영체제 - 가상 메모리의 이해 - 페이징 폴트
운영체제 - 가상 메모리의 이해 - 페이지 교체 알고리즘
소프트웨어 베이직 - 자료구조와 알고리즘 - 17. 그래프 - 너비 우선 탐색
- 너비 우선 탐색 (Breadth Frist Search)
너비를 우선으로 하는 탐색 알고리즘
Queue 자료구조를 기반으로 한다.
고급 그래프 탐색 알고리즘에서 자주 활용되기 때문에
고급 개발자가 되기 위해서 너비 우선 탐색을 숙지할 필요가 있다.
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드들을 모두 큐에 삽입하고, 방문 처리
3. 2의 과정을 더 이상 수행할 수 없을 때까지 반복

위의 그림을 1부터 시작해서 너비 우선 탐색을 수행하면
방문 순서 : 1->2->3->8->7->4->5->6 이 된다.
-> 큐 자료구조를 기반으로 하기 때문에 구현이 간단한 편이다.
실제로 큐 STL을 이용하면 훨씬 더 간단히 구현할 수 있다. (cpp에서 다룰 예정)
시간 복잡도는 O(N)이며,
일반적으로 DFS보다 수행 시간이 더 짧은 편이다.
- 너비 우선 탐색 구현하기
* 너비 우선 탐색 - 연결 리스트 정의

* 너비 우선 탐색 - 연결 리스트 삽입 함수

* 너비 우선 탐색 - 큐 삽입 함수
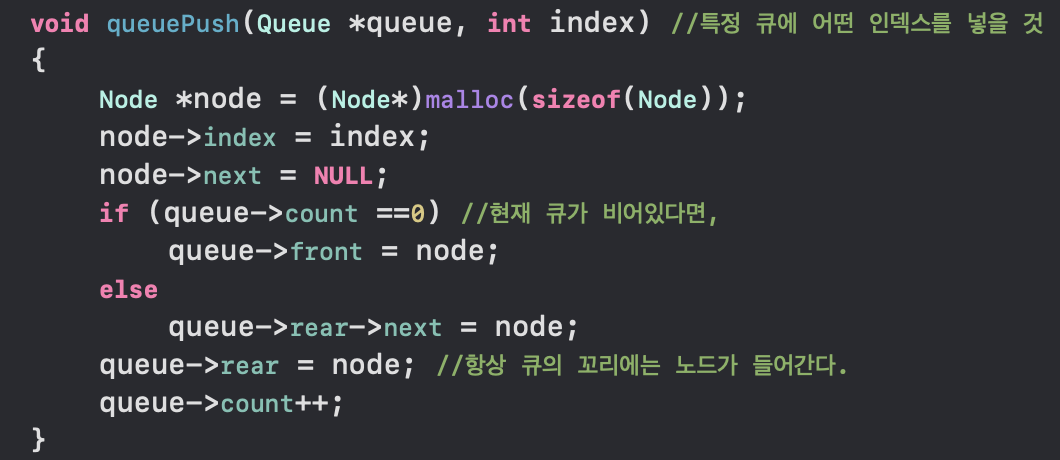
* 너비 우선 탐색 - 큐 추출 함수

* 너비 우선 탐색 - 너비 우선 탐색 함수

* 너비 우선 탐색 - 이용해보기

위의 코드들을 이용해
간단한 너비 우선 탐색 프로그램을 실행해 보았다.
node : 5, edge : 4
연결된 부분은
1-2
1-3
1-5
2-5
라고 입력했을 때
연결되지 않은 노드인 4를 제외하고
방문한 노드들을 정상적으로 출력하는 것을 확인할 수 있다.
(방문 순서에 대한 부분은 작성되지 않았으므로 코드 작성 이전에 보았던 예제와는 결과가 다르다.)

소프트웨어 베이직 - 자료구조와 알고리즘 - 18. 탐색 - 이진 탐색 트리
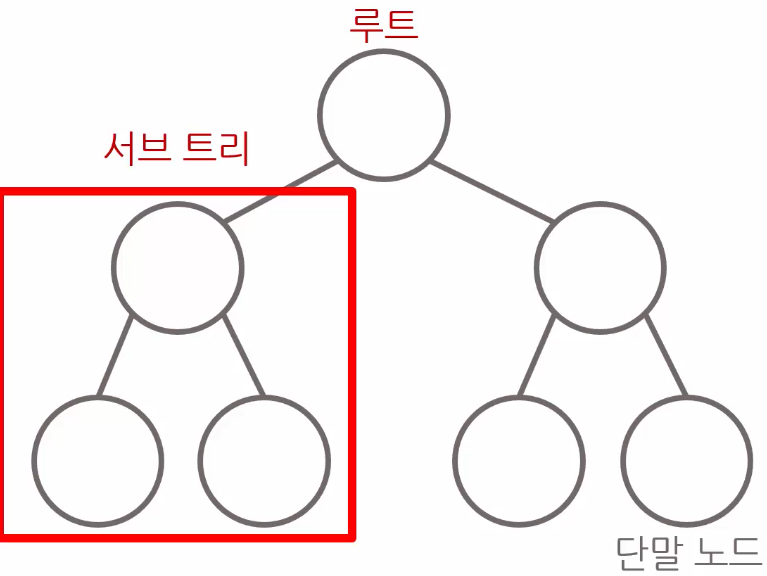
- 이진 탐색 트리 (Binary Search Tree)
이진 탐색(binary search)이 항상 동작하도록 구현하여 탐색 속도를 극대화시킨 자료구조
-> 항상 부모노드가 왼쪽 자식보다는 크고, 오른쪽 자식보다는 작다.
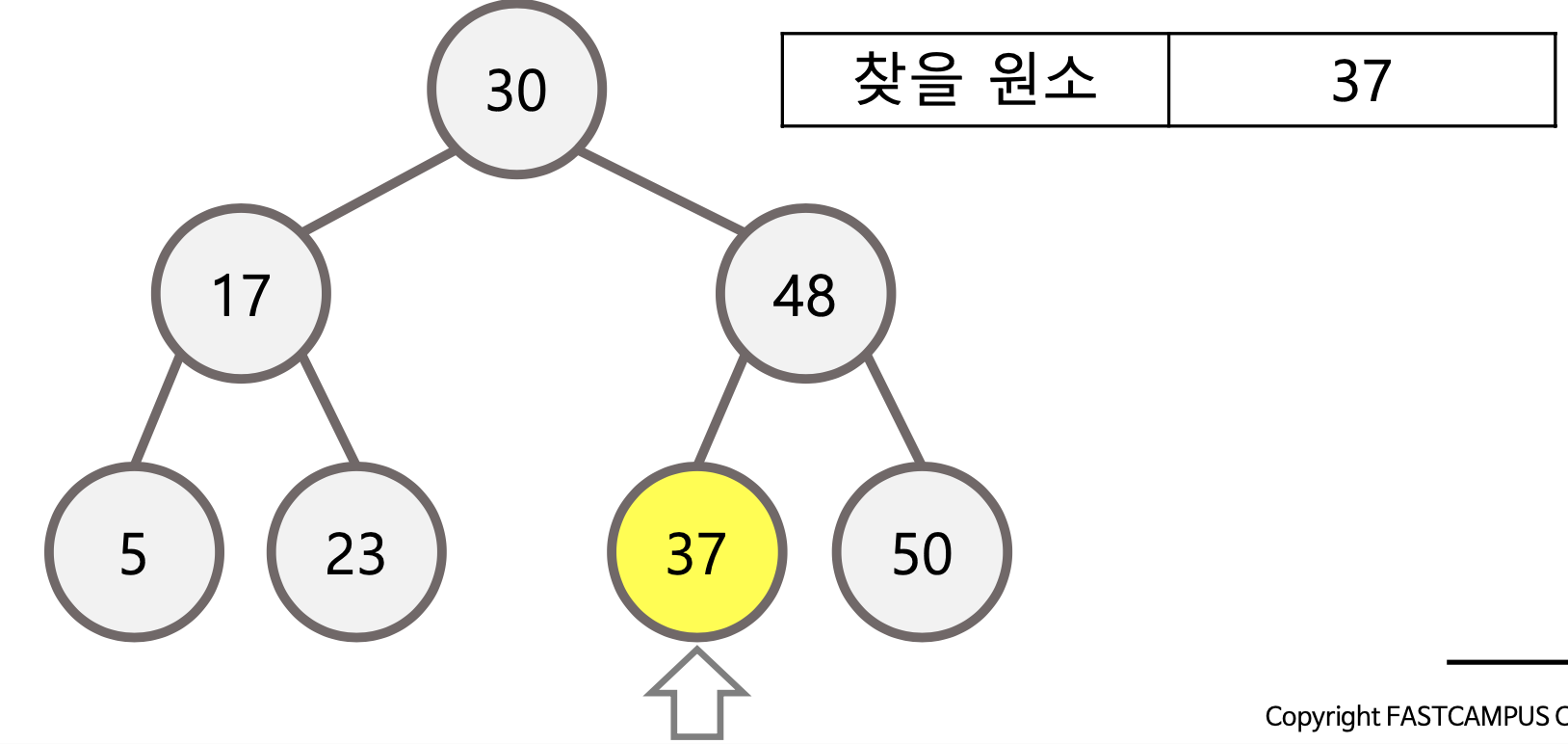
위의 예제를 살펴보았을 때,
root(30)에서부터 출발해서 '37'을 찾고자 한다.
부모보다 큰 값은 오른쪽에 있을 것이므로 곧바로 오른쪽 자식으로 향한다.
-> 왼쪽 노드들은 볼 필요가 없어진다.
48과 비교해서 찾고자 하는 값이 더 작으므로 왼쪽 자식으로 향하면
곧바로 37을 찾을 수 있다.
이 예제의 경우 가짓수가 적기 때문에
탐색 속도가 극대화되었다는 느낌을 받지 못할 수도 있지만,
가짓수가 많아질 수록 다른 알고리즘과의 차이점을 느낄 수 있을 것이다.
=>
이진 탐색 트리에서 탐색을 할 때는
찾고자 하는 값이 부모 노드보다 작을 경우 왼쪽 자식으로,
찾고자 하는 값이 부모 노드보다 클 경우 오른쪽 자식으로 이어나가며 방문하게 된다.
한 번 확인할 때마다 봐야 하는 원소의 갯수가 절반씩 줄어들기 때문에
'완전 이진 트리'의 경우 O(logN) 의 시간 복잡도를 갖게 된다.
- 이진 탐색 트리의 구현
* 이진 탐색 트리 정의

* 이진 탐색 트리의 삽입
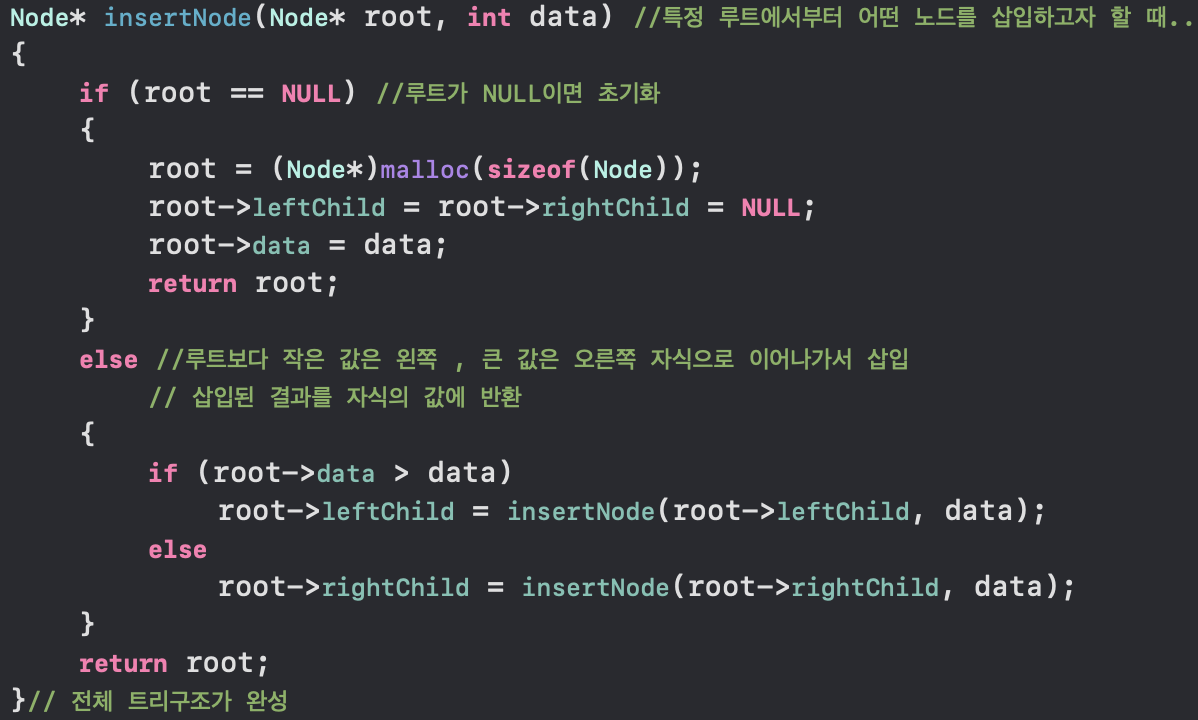
* 이진 탐색 트리의 탐색

* 이진 탐색 트리의 순회

전위 순회 방식으로 구현했는데,
후위 순회 방식으로 한 번 작성해보는 것도 좋을 듯
* 이진 탐색 트리의 삭제
** 자식이 없는 경우
단순히 제거
** 자식이 하나만 존재
삭제할 노드의 자리에 자식 노드를 넣는다.
** 자식이 둘 다 존재
삭제할 노드의 자리에 자기 다음으로 큰 노드를 넣는다.

위의 예시에서
30을 삭제하고자 한다면,
30보다 바로 다음으로 큰 값인 '37'을 '30'의 자리에 넣어야 한다.
** 이진 탐색 트리에서 가장 작은 원소를 찾는 함수 == 결과적으로 가장 왼쪽에 있는 함수를 찾음
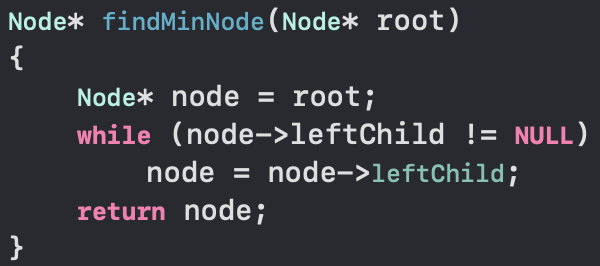
------본론으로 돌아와서, 이진 탐색 트리의 삭제 함수

삭제함수는 매우... 흥미로웠다.
37 17 4 23 48 50
* 이진 탐색 트리 이용해보기

위와 같이 메인함수를 작성해서 실행해보면

성공적으로 원하는 결과값을 얻을 수 있다.
정리
•완전 이진 트리에 가깝게 설계해야 이진 탐색 트리의 성능을 최대로 이끌어낼 수 있다.
(root node부터 시작해서 왼쪽 자식, 오른쪽 자식 노드 순으로 차례대로 들어가는 구조)
** 완전 이진트리에서는 어떤 요소의 탐색에도 O(logN)의 시간이 소요된다.
** 편향 이진트리에서는 시간 복잡도가 O(N)이므로, 오히려 배열을 사용하는 것보다 비효율적이다.
•트리의 효율성
트리에서 데이터의 갯수가 N개일 때, O(N)의 공간이 소요되며,
삽입 및 삭제의 경우 일반적으로 기존의 배열(array)을 이용하는 것보다 효율적이다.
=> DB 등 대용량 저장 및 검색 자료구조로 많이 활용된다.
운영체제 - 가상 메모리의 이해 - 페이징 시스템
운영체제 - 가상 메모리의 이해 - 다중 단계 페이징 시스템과 페이징 시스템 장점
운영체제 - 가상 메모리의 이해 - 페이징 폴트
운영체제 - 가상 메모리의 이해 - 페이지 교체 알고리즘
올인원 패키지 : 컴퓨터 공학 전공 필수👉https://bit.ly/3i4sCVE
'패스트캠퍼스' 카테고리의 다른 글
| 자료구조/알고리즘 - AVL 트리 (0) | 2020.12.15 |
|---|---|
| 운영체제 - 가상 메모리 (0) | 2020.12.10 |
| [패스트캠퍼스 수강 후기] 올인원 패키지 : 컴퓨터 공학 전공 필수👉C언어인강 100% 환급 챌린지 49회차 미션 (0) | 2020.12.06 |
| [패스트캠퍼스 수강 후기] 올인원 패키지 : 컴퓨터 공학 전공 필수👉C언어인강 100% 환급 챌린지 48회차 미션 (0) | 2020.12.05 |
| [패스트캠퍼스 수강 후기] 올인원 패키지 : 컴퓨터 공학 전공 필수👉C언어인강 100% 환급 챌린지 47회차 미션 (0) | 2020.12.04 |